Unity - Shader - 矩阵

矢量的点积

矢量之间可以进行乘法

公式 1:

a·b = (ax,ay,az)·(bx,by,bz) = ax*bx + ay*by + az*bz

点积的其中一个几何意义是投影

假设，有一个单位矢量 a 和另一个长度不限的矢量 b。现在 ，我们希望得到 b 在平行于 a 的一条直线上的投影 。那么，我们就可以使用点积 a·b 来得到 b 在 a 方向上的有符号的投影。

给一个通俗的解释。我们可以认为，现在有一个光源，它发出的光线是垂直于 a 方向的，那么 b 在 a 方向上的投影就是 b 在 a 方向上的影子。

公式 2:

a·b=|a||b|cos0

矢量的叉积

公式：

aXb=(ax,ay,az)X(bx,by,bz)=(ay*bz-az*by,az*bx-ax*bz,ax*by-ay*bx)

|aXb|=|a||b|sin0

叉积的几何意义是垂直于 a 和 b 所形成的平面的矢量

矩阵运算

矩阵和矩阵的乘法

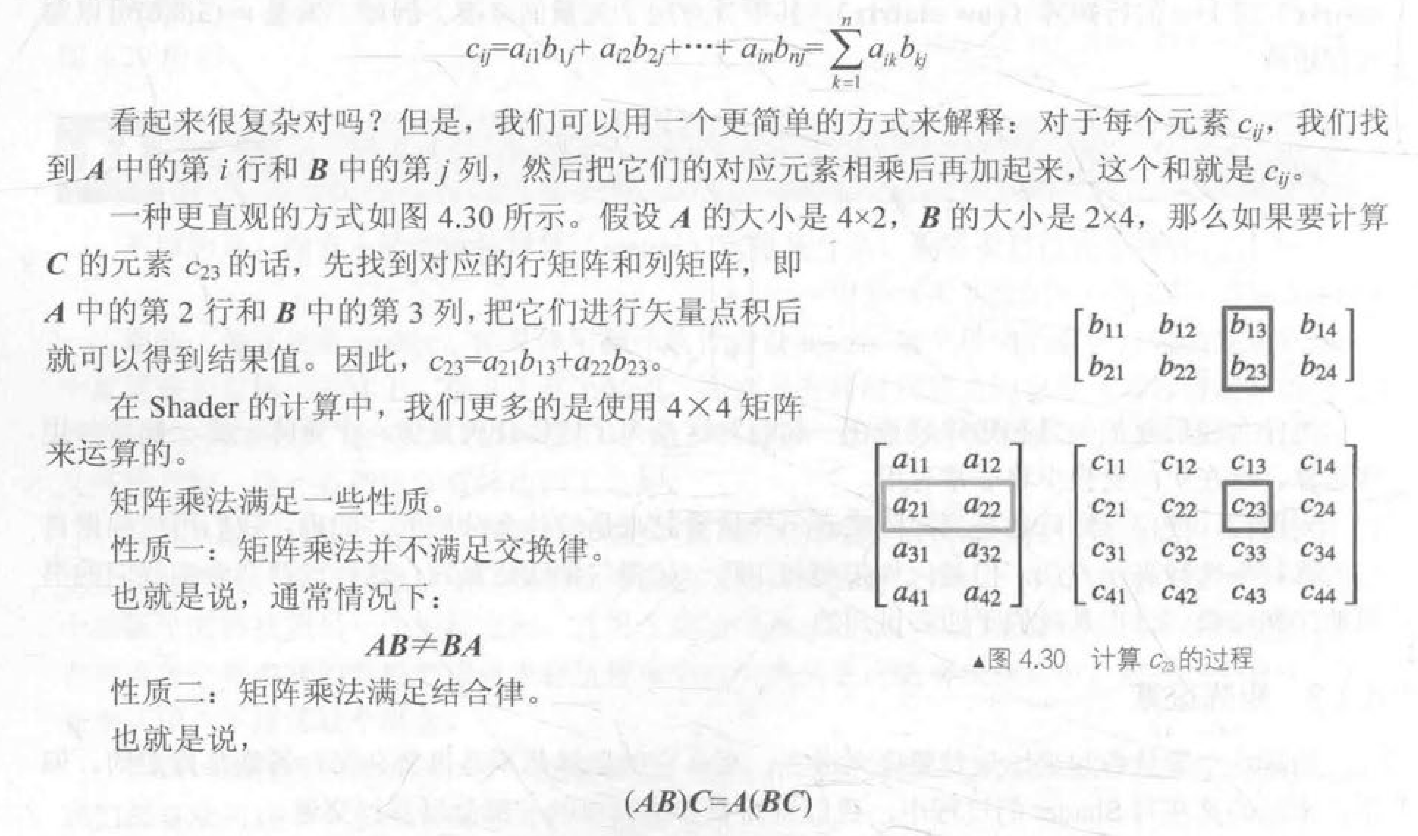
第一个矩阵的列数必须等于第二个矩阵的行数，它们相乘得到的结果是一个新的矩阵，新矩阵的行数等于第一个矩阵的行数，新矩阵的列数等于第二个矩阵的列数。
例如：矩阵 A 4x3，矩阵 B 3x6，那么矩阵 A 和矩阵 B 相乘得到的结果是一个新的矩阵，即 4x6
(A 行乘 B 列)